When it comes to modern web application development, MongoDB is the king. If you are a full stack programmer, you hear about MERN or MEAN stacks every day. The M is in every one of them and it stands for MongoDB. The free and open source community version of MongoDB powers a large number of Web applications. From its humble beginnings in 2007, MongoDB has come a long way. It is the primary product behind the company MongoDB Inc. with over 10 billion dollars in market capitalisation. Like many other products before and after, online advertising was the key catalyst behind the vision and development of MongoDB. The story of MongoDB is an interesting one and in this article, I will take you on a journey through the MongoDB land and its history.

The Idea of the Humongous Database - The Beginnings

The story of MongoDB has its beginnings much earlier than 2007. In 1995, Dwight Merriman and Kevin O'Connor created the famous online advertising company DoubleClick. Kevin Ryan joined the team soon after(Dwight and Kevin later cofounded 5 companies together - Gilt, 10gen, Panther Express, ShopWiki and Business Insider). DoubleClick soon took off and within a few years it was serving as much as 400,000 ads/second. Such large scale traffic was not anticipated by the relational database technologies available at that time. Configuring relational databases for such scale also required substantial amount of money and hardware resources. So Dwight(who was the CTO at the time) and his team wrote custom database implementations to scale DoubleClick for the increased traffic. In one of his early talks on MongoDB, Dwight talks about getting a network hardware with serial number 7 and wondering whether it will work! This was even before the invention of load balancers.

In 2003, Eliot Horowitz joined DoubleClick R&D division as a software engineer immediately after his college. Within 2 years he left DoubleClick to start ShopWiki along with Dwight. Both of them realised that they were solving the same horizontal scalability issues again and again. So in 2007, Dwight, Eliot and Kevin Ryan started a new company called 10gen. 10gen was focused on creating a PaaS hosting solution with its own application and database stack. 10gen soon got the attention of the venture capitalist Albert Wenger (Union Square Ventures) and he invested $1.5 million into it. This is what Albert Wenger wrote in 2008 about the 10gen investment,

Today we are excited to announce that we are backing a team working on an alternative, the amazingly talented folks at 10gen. They bring together experience in building Internet scale systems, such as DART and the Panther Express CDN, with extensive Open Source involvement, including the Apache Software Foundation. They are building an open source stack for cloud computing that includes an appserver and a database both written from scratch based on the capabilities of modern hardware and the many lessons learned in what it takes to build a web site or service. The appserver initially supports server side Javascript and (experimentally) Ruby. The database stores objects using an interesting design that balances fast random access with efficient scanning of collections.

What Albert was refering to as "the database with interesting design" was in fact MongoDB. Rapid development on the new database was undertaken from 2007 to 2009. The first commit of the MongoDB database server by Dwight can be seen here. The core engine was written in C++. The database was named MongoDB since the idea was to use it to store and serve humongous amount of data required in typical use cases such as content serving. Initially the team had only 4 engineers(including Dwight and Eliot) and decided to focus just on the MongoDB database instead of the initial PaaS product. The business idea was to release the database as an open source free download and offer commercial support and training services on top of it.

MongoDB 1.0 was released in February 2009. The initial version focused on providing a usable query language with document model, indexing and basic support for replication. It also had experimental version of sharding, but production ready sharding clusters were available only in version 1.6 released a year later.

Here is how Dwight responded to a question on the suitability of Mongo for a highly scalable system (MongoDB user group - September 2009),

For horizontal scaling, one would use auto-sharding to build out large MongoDB clusters. This is in alpha now, but if your project is just getting started, it will be in production by the time you need it.

Early MongoDB Design Philosophy

In the early years, the basic design principles behind MongoDB development were the following,

• Quick and easy data model for faster programming - document model with CRUD.
• Use of familiar language and format - JavaScript/JSON.
• Schema less documents for agile iterative development.
• Only essential features for faster development and easy scaling. No join, no transactions across collections.
• Support easy horizontal scaling and durability/availability (replication/sharding).

In his ZendCon 2011 presentation titled "NoSQL and why we created MongoDB", Dwight talks about these principles in detail. Around 42 minutes mark, there is also an interesting discussion on the difference between replication and sharding. As the database server code matured and once MongoDB hit the mainstream, many of these principles were obviously diluted. Latest MongoDB server versions support joining to some extend and since MongoDB 4.2, even distributed transactions are supported!

What is MongoDB?

Before we get into detailed MongoDB history and how it evolved over the years, let us briefly look at what exactly it is!

MongoDB is a document based NoSQL database. It can run on all major platforms (Windows, Linux, Mac) and the open source version is available as a free download. MongoDB stores data entities in a container called collection and each piece of data stored is in a JSON document format. For example, if a customer submits an online order, the entire details of that order (order number, order line items, delivery address etc.) are kept in a single hierarchical document in JSON format. It is then saved to a collection named "customer_order".

MongoDB also comes with a console client called MongoDB shell. This is a fully functional JavaScript environment using which you can add, remove, edit or query document data in the database.

MongoDB Architecture

The following MongoDB architecture diagram provides a high level view of the major components in the MongoDB server.

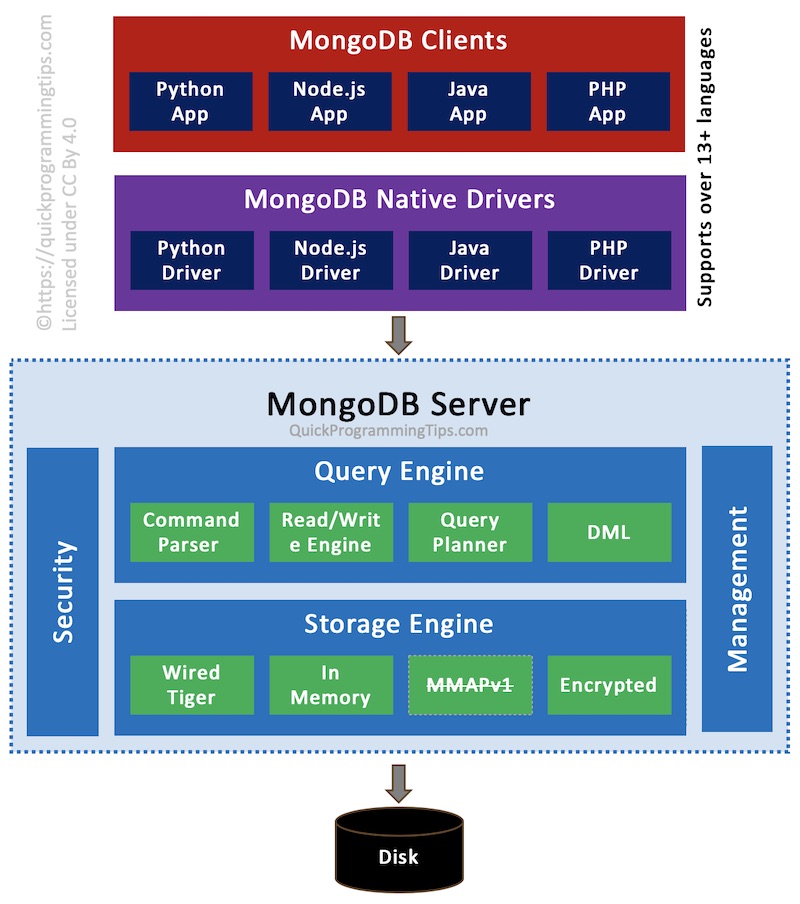
MongoDB currently offers drivers for 13 languages including Java, Node.JS, Python, PHP and Swift. The storage engine MMAPv1 is removed since version 4.2. The encrypted storage engine is only supported in the commercial enterprise server.

The beauty of MongoDB is that using the same open source free community server you can,

• Run a simple single machine instance suitable for most small applications.
• Run a multi-machine instance with durability/high availability suitable for most business applications.
• Run a large horizontally scaled cluster of machines(shard cluster) handling both very large sets of data and high volume of query traffic. MongoDB provides automatic infrastructure to distribute both data and its processing across machines. A typical use case would be running a popular ad service with thousands of customers and millions of impressions.

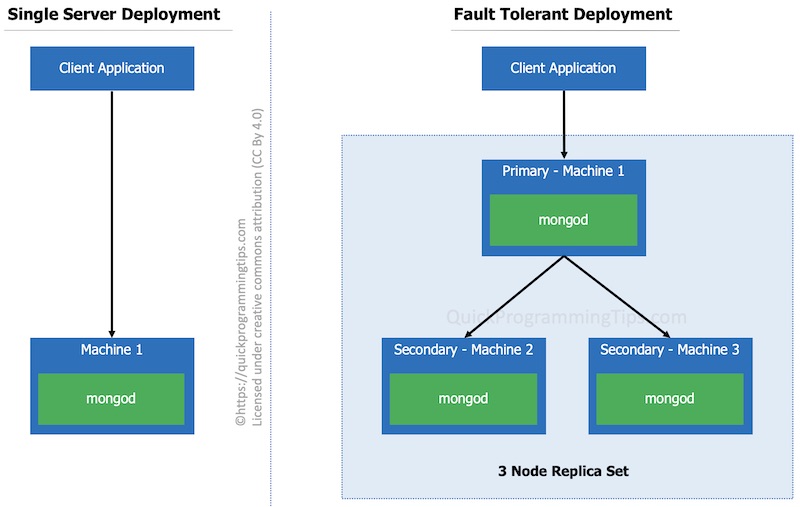
The following diagrams show various options available for running MongoDB instances.

Single Server/Fault Tolerant Setup

For small applications, a single server setup is enough with frequent data backups. For installations that require fault tolerance, a replica set implementation can be done. In the fault tolerant deployment, usually there are 3 or more MongoDB instances. Only one of them work as the primary instance and if it fails, one of the other 2 secondaries takes over as the primary. The data is identical in all instances.

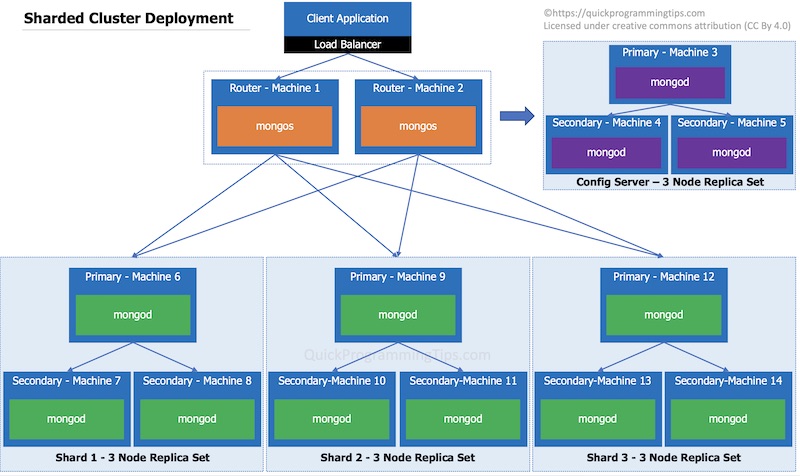
Shard Cluster for Horizontal Scalability

For a large database with both horizontal scalability and fault tolerance requirements, a MongoDB shard cluster is configured. As can be seen from the diagram below, minimum recommended number of machines for a fault tolerant shard cluster is 14! Each fault tolerant replica set in this case handles only a subset of the data. This data partitioning is automatically done by MongoDB engine.

When you download the latest version of MongoDB (4.4) and extract it, you will find that it contains only the following 3 main files,

• mongo - MongoDB shell for interacting with your server using JavaScript based commands.
• mongod - The MongoDB main executable. This can run as a single database instance, as a database member of a sharded cluster or as a configuration server of a sharded cluster.
• mongos - A router application only needed for sharded horizontally scaled cluster of database servers.

In a mac machine, the total size of these 3 executables is around 150MB. These are the only components you need for any type of MongoDB deployments! In a world of bloated software, this is a welcome change! This simplicity and elegance is what makes MongoDB so powerful and reliable.

Evolution of MongoDB (2009 to 2020)

MongoDB 1.0 was released in February 2009 and it had most of the basic query functionalities. MongoDB 1.2 was released in December 2009 and it introduced large scale data processing using map-reduce. Realising that MongoDB has good potential, 10gen quickly ramped up the team. MongoDB 1.4 (March 2010) introduced background index creation and MongoDB 1.6 (August 2010) introduced some major features such as production ready sharding for horizontal scaling, replica sets with automatic failover and IPv6 support.

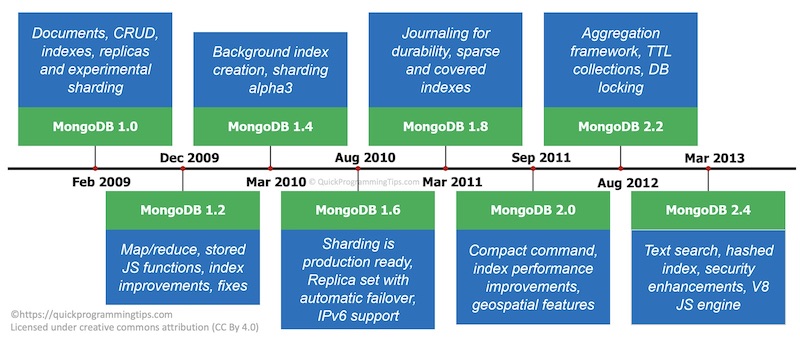
By 2012, 10gen had 100 employees and the company started providing 24/7 support. MongoDB 2.2 release(August 2012) introduced aggregation pipeline enabling multiple data processing steps as a chain of operations. By 2013, 10gen had over 250 employees and 1000 customers. Realising the true business potential, 10gen was renamed as MongoDB Inc. to focus fully on the database product. MongoDB 2.4 release (March 2013) introduced text search and Google's V8 JS engine in Mongo shell among other enhancements. Along with 2.4, a commercial version of the database called MongoDB Enterprise was released. It included additional features such as monitoring and security integrations.

One of the major problems with early MongoDB versions was its relatively weak storage engine used for saving and managing the data on the disk. MongoDB Inc.'s first acquisition was WiredTiger, a company behind the super stable storage engine with the same name. MongoDB acquired both the team and the product and its main architect Michael Cahill(also one of the architects of Berkeley DB) became director of engineering(storage) in the company. WiredTiger is an efficient storage engine. Using a variety of programming techniques such as hazard pointers, lock-free algorithms, fast latching and message passing, WiredTiger performs more work per CPU core than alternative engines. To minimize on-disk overhead and I/O, WiredTiger uses compact file formats, and optionally, compression.

Next major release of MongoDB was 3.0 (March 2015) which featured the new WiredTiger storage engine, pluggable storage engine API, increased replica set member limit of 50 and security improvements. The same year Glassdoor featured MongoDB Inc. as one of the best places to work. Later in the year version 3.2 was released and it supported document validation, partial indexes and some major aggregation enhancements.

In 2017, Microsoft released a proprietary, globally distributed, multi-model NoSQL database service called CosmosDB as part of the Microsoft Azure cloud platform. This offered protocol compatibility with MongoDB 3.2 so that queries written in MongoDB 3.2 could be run on CosmosDB. I think this accelerated the adoption of CosmosDB among developers.

By 2016, MongoDB Inc. had 500 employees and the database itself was downloaded over 20 million times. In October 2017, MongoDB Inc. went public with over 1 billion dollars in market capitalisation. MongoDB 3.6 was released a month later(November 2017) and it included better support for $lookup for multi-collection joins, change streams and $jsonSchema operator to support document validation using JSON Schema. Notably MongoDB 3.6 is the latest version supported by Microsoft Azure CosmosDB as of August 2020.

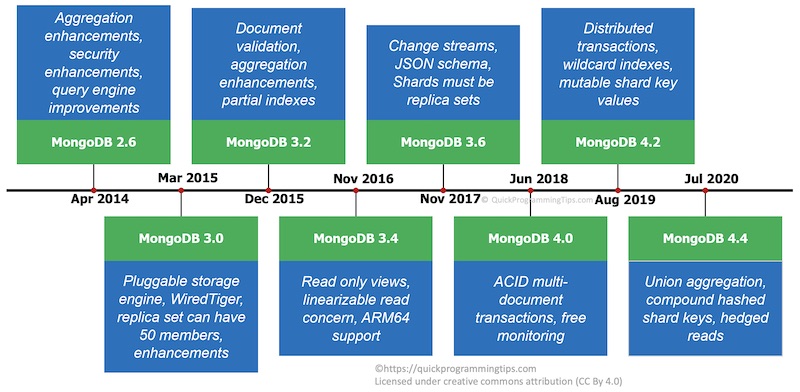
In 2018, MongoDB Inc. went for its second acquisition by taking over mLab for 68 million dollars. At the time mLab was providing MongoDB as a service(DBaaS) on the cloud and had a large number of customers. Cloud was the future and MongoDB Inc. moved quickly to acquire and integrate mLab as part of the MongoDB Atlas cloud platform. They then decided to address the issue of more competitors appearing in DBaaS space by changing the licensing terms of the open source version!

MongoDB open source community version and the premium enterprise version were both powered by the same underlying engine. This meant that anyone can take the community version and then offer a paid cloud version on top of it. This was a major problem for MongoDB Inc. since it meant direct competition for their cloud product, MongoDB Atlas. So in a controversial move, MongoDB Inc. changed the license of the community version from GNU AGPLv3 (AGPL), to Server Side Public License(SSPL) in October 2018. The license had a clause to prevent future SaaS competitors to use MongoDB and offer their own SaaS version,

If you make the functionality of the Program or a modified version available to third parties as a service, you must make the Service Source Code available via network download to everyone at no charge, under the terms of this License.

This was a license written by MongoDB Inc. itself and they claimed it is an OSI compliant license. The license was later withdrawn from the approval process of Open Source Initiative(OSI), but the open source version is still licensed under SSPL.

By 2018, the company had over 1000 employees. Next major release MongoDB 4.0 (June 2018) came with the capability to have transactions across multiple documents. It was a major milestone and MongoDB was getting ready for use cases with high data integrity needs.

The cloud ecosystem was rapidly growing and soon MongoDB Inc. realised the need for a full fledged cloud platform instead of just offering the database service. In 2019, MongoDB Inc. went for its third acquisition by taking over Realm, a cloud based mobile database company for $39 million. This was interesting since MongoDB originally started as a PaaS hosting solution and after 12 years, it was back on the same direction. In the same year MongoDB 4.2 was released with distributed transaction support.

The current version of MongoDB community server as of August 2020 is MongoDB 4.4. It is notable for the separation of MongoDB database tools as a separate download. MongoDB 4.4 contains some major feature enhancements such as union aggregation from multiple collections, refinable/compound hashed shard keys and hedged reads/mirrored reads.

MongoDB Today

As of 2020, MongoDB is downloaded 110 million times worldwide. MongoDB Inc. currently has 2000+ employees and has over 18,000 paying customers many of whom will be using both MongoDB Atlas and MongoDB Enterprise. The current version of MongoDB community server as of August 2020 is MongoDB 4.4. Most large companies must be using the community version internally for some use case. MongoDB community server is still open source and except some key features, it is still on par with MongoDB enterprise.

MongoDB enterprise server (seems to be priced around the range of $10k per year per server) offers the following additional features,

In addition to the community server, MongoDB Inc. offers the following products,

• MongoDB Database Tools - A collection of command line tools for working with a MongoDB installation. This includes import/export(mongodump, mongorestore, etc.) and diagnostic tools (mongostat, mongotop).
• MongoDB Enterprise Server - The enterprise version with additional security and auditing features.
• MongoDB Atlas - A premium cloud based SaaS version of the MongoDB server.
• Atlas Data Lake - A cloud based data lake tool powered by MongoDB query language that allows you to query and analyse data across MongoDB Atlas and AWS S3 buckets.
• Atlas Search - A cloud based full-text search engine that works on top of MongoDB Atlas.
• MongoDB Realm - A managed cloud service offering backend services for mobile apps.
• MongoDB Charts - A cloud tool to create visual representations of MongoDB data.
• MongoDB Compass - Downloadable GUI tool for connecting to the MongoDB database and querying data.
• MongoDB Ops Manager - On-premise management platform for deployment, backup and scaling of MongoDB on custom infrastructure.
• MongoDB Cloud Manager - The cloud version of the Ops manager.
• MongoDB Connectors - A set of drivers for other platforms/tools to connect to MongoDB.

The Road Ahead

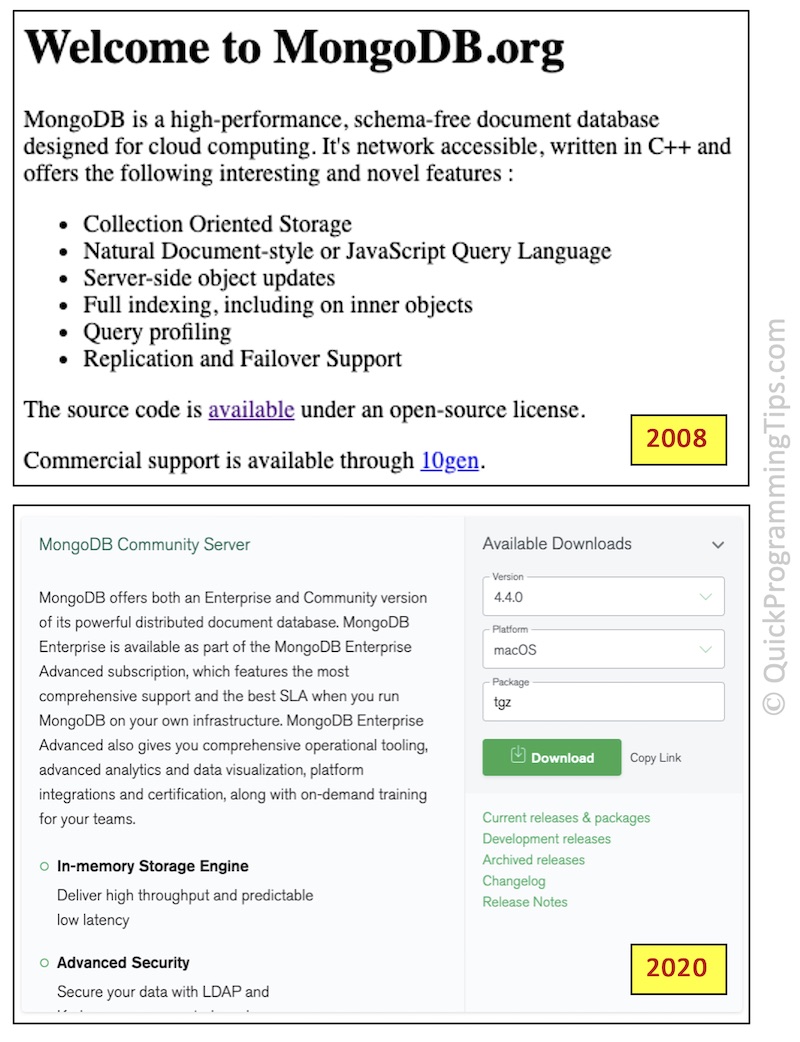
Since the SSPL license controversy, some among the developer community are wary of the MongoDB ecosystem. There is also the investor pressure to generate revenue around the eco-system. This is very evident if you consider the home page of MongoDB side by side between 2008 version and 2020 version (see image below). The MongoDB community server download page is actually showing the features available in the commercial enterprise version!

There is also heavy competition from Cloud vendors who are offering competing products. The main problem for MongoDB Inc. is that data storage is just one part of the enterprise application landscape. Without a compelling full stack of cloud services, MongoDB may find it hard in future to compete with cloud vendors.

Eliot Horowitz (a key figure behind MongoDB) left the company in July 2020. He seems to be still in an advisory role, but there is a risk of the product loosing its focus, reduced support for the free community version or further changes in licensing terms.

My Thoughts

MongoDB is a perfect example of how successful companies are formed based on a focused open source technology product. It is also a brilliant example of how to pivot at the right time in a product lifecycle. With its simplicity and small install footprint, MongoDB server demonstrates that it is still possible to build complex software without adding a lot of overhead. I hope that MongoDB Inc. will continue to support the community version in the coming years.

References/Further Reading

• Story of MongoDB Inc.
• MongoDB Community Server Github Repository
• MongoDB SSPL License
• Hacker News Discussion on SSPL
• MongoDB 4.4 Features
• MongoDB Inc. IPO Filing
• MongoDB: A Light in the Darkness! (2009 Article)
• MongoDB Google User Group(Archived)
• NoSQL and Why we created MongoDB(Video)
• Dwight and Kevin Interview (2013 Video)

When working with MongoDB collections, sometimes you may want to find the document that contains the longest array. For example, you may have a collection for storing shirts and the array "sizes" in it may contain all the sizes in which the shirt is available. In this case, how do you find the shirts with largest number of sizes? In other words, what is the shirt model with largest choice of sizes?

Let us assume that we use the collection "shirts" to store our shirt models available for sale. Let us populate it with some sample data.

db.shirts.insertMany([
{ "_id" : 1, "name" : "Blue Shirt", sizes: [ "S", "M", "L"] },
{ "_id" : 2, "name" : "Stripped Shirt", sizes: [ "S", "M", "L","XL","XXL"] },
{ "_id" : 3, "name" : "Black Shirt", sizes: [ "S", "M", "L","XL","XXL","XXXL"] },
{ "_id" : 4, "name" : "Grey Shirt", sizes: [ "S", "M", "L","XXL"] },
{ "_id" : 5, "name" : "Green Shirt", sizes: [ "S", "M", "L"] },
]);

From the data, it is clear that the Black shirt has the largest number of sizes. How do you find this using a MongoDB query? We can use the MongoDB aggregation with pipeline operations to get the document with the longest array. The following script returns the document id containing Black shirt which has the largest number of sizes.

db.shirts.aggregate( [
  { $unwind : "$sizes" },
  { $group : { _id : "$_id", length : { $sum : 1 } } },
  { $sort : { length : -1 } },
  { $limit : 1 }
] )

How does the above script work? Here is what happens,

• The $unwind pipeline deconstructs an array field from the input documents to output a document for each element
• The $group pipeline groups the documents based on _id
• The $sum computes number of documents after grouping (due to _id grouping this becomes array size)
• The $sort pipeline sorts in descending order of array length
• Finally $limit returns the document id with largest array and size of array

MongoDB collections are usually schema less. This means that a collection can potentially contain documents with different structure. Even if they are same, since data stored is different, document size can substantially vary. Sometimes you may want to find the largest document in a MongoDB collection. This is required if you are planning to migrate your MongoDB database to a cloud database such as Azure CosmosDB which has restrictions on the maximum size of a single document in a collection (currently it is 2MB).

How to Find the Largest Document in a MongoDB Collection?

The following script finds the largest document in a collection. The following example uses the "user" collection in my database. Replace it with your collection name.

var max = 0, id = null;

// iterate through each document
db.store.find().forEach(doc => {
    var size = Object.bsonsize(doc);
    if(size > max) {
        max = size;
        id = doc._id;
    }
});

// document id and size of the largest doc in bytes
print(""+id+", "+max);

Note that the above script loads every document in the collection to compute its size. Hence this can be very slow in large collections.

How to Find the Largest Document in a MongoDB Database Across Collections?

The following script finds the largest document across all collections in the MongoDB database. It prints the collection name, document id and size in bytes as output. For large databases, this may take minutes or even hours. Also note that it loads every document to compute size and hence can incur lot of network traffic.

var max = 0, id = null, c = null ;

// Iterate through all the collections!
db.getCollectionNames().forEach(function(cName) {

    // Now iterate through each document in the collection
    db[cName].find().forEach(doc => {
        var size = Object.bsonsize(doc);
        if(size > max) {
            max = size;
            id = doc._id;
            c = cName
        }
    });
});

// Collection name, document id and size of the largest doc in bytes
print(c+", "+id+", "+max);

If you are using MongoDB 4.4 or later, you can simply use the new aggregation operator $bsonSize to find the size of the document. It will substantially speed up the computation.

If you have a large MongoDB database in production with a large of number of collections and indexes, you may need to periodically analyse the size of them. Here are a few MongoDB script snippets that you may find useful.

How to Get Sorted List of MongoDB Collections by Size?

The following script sorts and prints collections by descending order of the size of collections. The size here refers to the total size in memory for all records in a collection. This is different from the storage size of the collection. Note that the size printed is in kilobytes.

var sizeArray = [];

// Find statistics of every collection and add to an array
db.getCollectionNames().forEach(function(cName) {
    sizeArray.push(db[cName].stats());
});

// Sort the stats array by size. The field 'size' is used
sizeArray = sizeArray.sort(function(a, b) { return b['size'] - a['size']; });

// Print output in kb
for (var stat in sizeArray) {
    print(sizeArray[stat]['ns'] + ": " + (sizeArray[stat]['size']/1024).toFixed(2) + " kb") ;
}

Following is the sample output,

testdb.store: 3797.75 kb
testdb.customer: 526.26 kb
testdb.user: 0.52 kb

In the above snippet, change column from "size" to "storageSize" if you want to sort by storage size.

How to Get Sorted List of All MongoDB Indexes by Size in a Database?

The following program iterates through all indexes of all collections and then sorts it in the descending order of the size of the index.

var sizeMap = {}

// Iterate through every collection
db.getCollectionNames().forEach(function(cName) {
   indexes = db[cName].stats().indexSizes

   // Now iterate through every index of the current collection
   // We create a map here with key as combination of collection name and index name
   for (i in indexes) sizeMap[cName + " - " + i] = indexes[i];
});

var sizeArray = [];

// Map is converted to an array each element of which is a two member array
// This inner arrary contains the collection+index name key and the size itself
for (key in sizeMap) sizeArray.push([key, sizeMap[key]])

// Now sort outer array using the second column of inner array
var sizeArray = sizeArray.sort(function(a, b) {return b[1] - a[1]})

// Print list of index size in sorted form
for (x in sizeArray) print( sizeArray[x][0] + ": " + (sizeArray[x][1]/1024).toFixed(2) +" kb");

Following is a sample output,

store - country_1_city_1: 848.00 kb
store - _id_: 448.00 kb
customer - _id_: 96.00 kb
customer - age_1: 80.00 kb
user - _id_: 32.00 kb

MongoDB is intended as a document storage database where we don't know all the fields required in a stored entity when we build an application. This means that MongoDB collections can contain documents with different schemas. Some documents may have additional keys or different keys compared to other documents. This flexibility allows for system to evolve rapidly since there is no constrained schema for the document.

However such flexibility and power comes with its own headaches. Since different documents can have different keys and structure, the application logic should be robust enough to handle all the combinations.

When an application is rapidly evolving and new documents are being added, we may need to get a consolidated view of all the keys present across the documents in a collection. The following script iterates through all the documents in the collection and creates a distinct set of top level keys used across them. You can use this to check if there is any key present in any document which you are not expecting in your application. Such a key may have been added by an intermediate production release of the application.

Script to Get Distinct Set of Top Level Keys of All Documents in a MongoDB Collection

Let us first create a sample collection named user which is intended to capture user details of an application. Let us create 3 documents which represents 3 releases of the application each progressively adding a new key to the document.

// create a user collection
db.createCollection("user");

// Initially user collection has 3 fields
db.user.insert({ name:"jack", 
email:"jack@quickprogrammingtips.com", age:40 });

// In release 2, we added a new field for title. Hence newer user records contain it
db.user.insert({ name:"tom", 
email:"tom@quickprogrammingtips.com", age:42, title:"mr" });

// In release 3, we added a new field for mobile number.
db.user.insert({ name:"ted", 
email:"ted@quickprogrammingtips.com", age:44, title:"mr", mobile:"99999999" });

When there are large number of changes in the data model across releases, we need a script to find the complete list of distinct keys across the documents in the collection. The following script finds all the distinct top level keys in our user collection.

var keys = {};

db.user.find().forEach(function(doc){
    for (var key in doc){
        if(!(key in keys)){
           keys[key] = key;
        }
    }
});

print(keys)

One limitation of the above script is that it only prints the top level keys of the document. The following MongoDB script prints the super set of all keys including the nested keys. However there are limitations when it comes to arrays.

How to Get Distinct Set of All Keys of All Documents in a MongoDB Collection

var keys = {};

// Recursive function to print all nested keys of a document
function getKeys(doc, keys, prefix) {
    for (var key in doc){
        // note that we are ignoring _id
        if(!(key in keys) && key!='_id'){

           if(typeof doc[key] == "object") {
               getKeys(doc[key],keys, prefix+key+".")
           }else {
               keys[prefix+key] = prefix+key;
           }
        }
    }
}

// print all keys. Replace "user" with your collection name.
db.user.find().forEach(function(doc) {
    getKeys(doc,keys,"")
});
print(keys)

Given the following document,

{
    "_id" : ObjectId("5f1b277b49eebe76ce081e19"),
    "name" : "jack",
    "email" : "jack@quickprogrammingtips.com",
    "age" : 40.0,
    "address" : {
        "line1" : "l1",
        "line2" : "l2"
    },
    "GlossSeeAlso" : [
        "GML",
        {
            "x" : "1"
        },
        "XML"
    ],
    "abc" : [
        {
            "id" : 28,
            "Title" : "Sweden"
        },
        {
            "id" : 56,
            "Title" : "USA"
        },
        {
            "id" : 89,
            "Title" : "England"
        }
    ]
}

The output is,

{
    "name" : "name",
    "email" : "email",
    "age" : "age",
    "title" : "title",
    "address.line1" : "address.line1",
    "address.line2" : "address.line2",
    "GlossSeeAlso.0" : "GlossSeeAlso.0",
    "GlossSeeAlso.1.x" : "GlossSeeAlso.1.x",
    "GlossSeeAlso.2" : "GlossSeeAlso.2",
    "abc.0.id" : "abc.0.id",
    "abc.0.Title" : "abc.0.Title",
    "abc.1.id" : "abc.1.id",
    "abc.1.Title" : "abc.1.Title",
    "abc.2.id" : "abc.2.id",
    "abc.2.Title" : "abc.2.Title",
    "mobile" : "mobile"
}

Note that the above function prints array indexes up to the highest one in all documents.